Approximately What Percentage Of The Data Lie Between 4 And 8 Hours?

Objective

Hither y'all will learn how to use the Empirical Rule to estimate the probability of an issue.

If the price per pound of USDA Option Beefiness is normally distributed with a mean of $iv.85/lb and a standard departure of $0.35/lb, what is the estimated probability that a randomly called sample (from a randomly called market) volition exist betwixt $5.xx and $5.55 per pound?

Watch This: Empirical Dominion

Guidance

This reading on the Empirical Rule is an extension of the previous reading "Understanding the Normal Distribution." In the prior reading, the goal was to develop an intuition of the interaction between decreased probability and increased altitude from the hateful. In this reading, we will practise applying the Empirical Rule to estimate the specific probability of occurrence of a sample based on the range of the sample, measured in standard deviations.

The graphic below is a representation of the Empirical Rule:

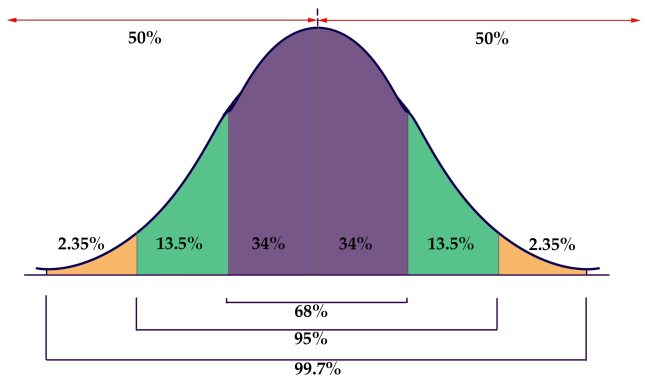
Figure5_3_1

The graphic is a rather concise summary of the vital statistics of a Normal Distribution. Note how the graph resembles a bell? Now you know why the normal distribution is also chosen a " bell curve."

50% of the data is higher up, and 50% below, the mean of the information
Approximately 68% of the data occurs within i SD of the mean
Approximately 95% occurs within ii SD's of the hateful
Approximately 99.7% of the data occurs inside iii SDs of the hateful

It is due to the probabilities associated with 1, 2, and iii SDs that the Empirical Rule is also known as the 68−95−99.7 rule.

Case 1

If the bore of a basketball game is normally distributed, with a mean (µ) of 9″, and a standard difference (σ) of 0.5″, what is the probability that a randomly called basketball will have a diameter between ix.v″ and 10.5″?

Solution

Since the σ = 0.five″ and the µ = nine″, we are evaluating the probability that a randomly chosen ball will have a diameter between i and 3 standard deviations above the hateful. The graphic below shows the portion of the normal distribution included betwixt ane and 3 SDs:

Figure5_3_2

The percentage of the data spanning the 2d and 3rd SDs is thirteen.5% + 2.35% = 15.85%

The probability that a randomly chosen basketball will accept a diameter betwixt 9.5 and 10.5 inches is 15.85%.

Example 2

If the depth of the snowfall in my yard is normally distributed, with µ = 2.five″ and σ = .25″, what is the probability that a randomly chosen location will have a snow depth between ii.25 and 2.75 inches?

Figure5_3_3

Solution

2.25 inches is µ − 1σ, and two.75 inches is µ + 1σ, so the area encompassed approximately represents 34% + 34% = 68%.

The probability that a randomly chosen location will have a depth between 2.25 and 2.75 inches is 68%.

Example 3

If the height of women in the United States is usually distributed with µ = 5′ eight″ and σ = one.5″, what is the probability that a randomly called woman in the Us is shorter than 5′ v″?

Solution

This i is slightly different, since nosotros aren't looking for the probability of a limited range of values. Nosotros want to evaluate the probability of a value occurring anywhere below 5′ 5″. Since the domain of a normal distribution is infinite, we can't actually state the probability of the portion of the distribution on "that end" considering it has no "end"! What we need to practice is add upwardly the probabilities that nosotros do know and subtract them from 100% to go the residual.

Hither is that normal distribution graphic once again, with the top information inserted:

Figure5_3_4

Recall that a normal distribution always has fifty% of the information on each side of the mean. That indicates that 50% of US females are taller than 5′ 8″, and gives us a solid starting bespeak to summate from. There is another 34% between v′ 6.five″ and v′ 8″ and a final thirteen.5% between 5′ 5″ and 5′ vi.v″. Ultimately that totals: 50% + 34% + 13.5% = 97.v%. Since 97.5% of United states females are v′ 5″ or taller, that leaves 2.v% that are less than 5′ 5″ tall.

Intro Problem Revisited

If the price per pound of USDA Choice Beef is normally distributed with a hateful of $4.85/lb and a standard difference of $0.35/lb, what is the estimated probability that a randomly chosen sample (from a randomly chosen market) will be between $5.20 and $5.55 per pound?

$5.xx is µ + 1σ, and $5.55 is µ + 2σ, so the probability of a value occurring in that range is approximately 13.5%.

Vocabulary

Normal distribution: a common, but specific, distribution of data with a ready of characteristics detailed in the lesson above.

Empirical Rule: a name for the way in which the normal distribution divides data by standard deviations: 68% within 1 SD, 95% within 2 SDs and 99.7 within 3 SDs of the mean

68-95-99.seven dominion: another name for the Empirical Rule

Bell curve: the shape of a normal distribution

Guided Practice

A usually distributed data set has µ = ten and σ = 2.5, what is the probability of randomly selecting a value greater than 17.5 from the prepare?
A normally distributed data set has µ = .05 and σ = .01, what is the probability of randomly choosing a value between .05 and .07 from the set?
A unremarkably distributed data gear up has µ = 514 and an unknown standard deviation, what is the probability that a randomly selected value will be less than 514?

Solutions

If µ = 10 and σ = 2.5, then 17.5 = µ + 3σ. Since we are looking for all information in a higher place that point, nosotros demand to subtract the probability that a value will occur below that value from 100%: The probability that a value will be less than 10 is 50%, since 10 is the mean. There is another 34% between ten and 12.v, another xiii.5% betwixt 12.5 and xv, and a final 2.35% between 15 and 17.5. 100% −50% −34% −xiii.5% −2.35% = 0.15% probability of a value greater than 17.v
0.05 is the mean, and 0.07 is 2 standard deviations above the mean, and then the probability of a value in that range is 34% + 13.5% = 47.v%
514 is the mean, so the probability of a value less than that is 50%.

Practice Questions

Assume all distributions to exist normal or approximately normal, and calculate percentages using the 68−95−99.vii rule.

Given mean 63 and standard deviation of 168, find the approximate percent of the distribution that lies between −105 and 567.
Approximately what per centum of a normal distribution is between 2 standard deviations and 3 standard deviations from the hateful?
Given standard divergence of 74 and mean of 124, approximately what percentage of the values are greater than 198?
Given σ = 39 and µ = 101, approximately what percentage of the values are less than 23?
Given hateful 92 and standard divergence 189, find the judge percentage of the distribution that lies between −286 and 470.
Approximately what percent of a normal distribution lies between µ + 1σ and µ + 2σ?
Given standard deviation of 113 and mean 81, approximately what percentage of the values are less than −145?
Given mean 23 and standard divergence 157, find the approximate pct of the distribution that lies betwixt 23 and 337.
Given σ = 3 and µ = 84, approximately what percentage of the values are greater than ninety?
Approximately what percent of a normal distribution is between µ and µ+1σ?
Given hateful 118 and standard deviation 145, find the approximate percentage of the distribution that lies between −27 and 118.
Given standard deviation of 81 and mean 67, approximately what percentage of values are greater than 310?
Approximately what percentage of a normal distribution is less than 2 standard deviations from the mean?
Given µ + 1σ = 247 and µ + 2σ = 428, detect the approximate percentage of the distribution that lies between 66 and 428.
Given µ − 1σ = −131 and µ + 1σ = 233, approximately what percentage of the values are greater than −495?