How To Deal With Different Seq Len Data In Keras

How to Develop a Bidirectional LSTM For Sequence Classification in Python with Keras

Concluding Updated on January 18, 2021

Bidirectional LSTMs are an extension of traditional LSTMs that can improve model performance on sequence classification problems.

In issues where all timesteps of the input sequence are available, Bidirectional LSTMs train ii instead of one LSTMs on the input sequence. The first on the input sequence as-is and the 2nd on a reversed re-create of the input sequence. This can provide additional context to the network and result in faster and even fuller learning on the problem.

In this tutorial, you will detect how to develop Bidirectional LSTMs for sequence classification in Python with the Keras deep learning library.

After completing this tutorial, you volition know:

How to develop a minor contrived and configurable sequence classification problem.
How to develop an LSTM and Bidirectional LSTM for sequence nomenclature.
How to compare the performance of the merge mode used in Bidirectional LSTMs.

Kick-start your project with my new book Long Short-Term Memory Networks With Python, including pace-by-step tutorials and the Python source lawmaking files for all examples.

Permit's get started.

Update January/2020: Updated API for Keras 2.3 and TensorFlow 2.0.

How to Develop a Bidirectional LSTM For Sequence Classification in Python with Keras
Photo by Cristiano Medeiros Dalbem, some rights reserved.

Overview

This tutorial is divided into half-dozen parts; they are:

Bidirectional LSTMs
Sequence Classification Trouble
LSTM For Sequence Classification
Bidirectional LSTM For Sequence Classification
Compare LSTM to Bidirectional LSTM
Comparing Bidirectional LSTM Merge Modes

Surroundings

This tutorial assumes you have a Python SciPy environment installed. You can utilise either Python 2 or 3 with this instance.

This tutorial assumes y'all have Keras (v2.0.4+) installed with either the TensorFlow (v1.one.0+) or Theano (v0.nine+) backend.

This tutorial too assumes you have scikit-learn, Pandas, NumPy, and Matplotlib installed.

If you need aid setting up your Python surround, see this post:

How to Setup a Python Environment for Machine Learning and Deep Learning with Anaconda

Need help with LSTMs for Sequence Prediction?

Take my free vii-day email course and notice 6 different LSTM architectures (with code).

Click to sign-up and also go a costless PDF Ebook version of the grade.

Bidirectional LSTMs

The idea of Bidirectional Recurrent Neural Networks (RNNs) is straightforward.

Information technology involves duplicating the outset recurrent layer in the network and so that at that place are at present two layers side-by-side, then providing the input sequence every bit-is as input to the offset layer and providing a reversed copy of the input sequence to the 2nd.

To overcome the limitations of a regular RNN […] nosotros propose a bidirectional recurrent neural network (BRNN) that tin be trained using all bachelor input information in the past and time to come of a specific time frame.

…

The idea is to split the country neurons of a regular RNN in a part that is responsible for the positive fourth dimension direction (forward states) and a part for the negative fourth dimension direction (astern states)

— Mike Schuster and Kuldip K. Paliwal, Bidirectional Recurrent Neural Networks, 1997

This approach has been used to keen effect with Long Brusk-Term Retentivity (LSTM) Recurrent Neural Networks.

The use of providing the sequence bi-directionally was initially justified in the domain of speech recognition because there is prove that the context of the whole utterance is used to interpret what is being said rather than a linear interpretation.

… relying on knowledge of the hereafter seems at kickoff sight to violate causality. How tin can we base our understanding of what we've heard on something that hasn't been said yet? However, man listeners practice exactly that. Sounds, words, and fifty-fifty whole sentences that at first mean nil are found to make sense in the lite of future context. What nosotros must recall is the distinction betwixt tasks that are truly online – requiring an output after every input – and those where outputs are simply needed at the end of some input segment.

— Alex Graves and Jurgen Schmidhuber, Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures, 2005

The use of bidirectional LSTMs may not make sense for all sequence prediction problems, only can offer some benefit in terms of better results to those domains where it is appropriate.

We have found that bidirectional networks are significantly more constructive than unidirectional ones…

— Alex Graves and Jurgen Schmidhuber, Framewise Phoneme Nomenclature with Bidirectional LSTM and Other Neural Network Architectures, 2005

To be clear, timesteps in the input sequence are even so processed one at a time, information technology is just the network steps through the input sequence in both directions at the same time.

Bidirectional LSTMs in Keras

Bidirectional LSTMs are supported in Keras via the Bidirectional layer wrapper.

This wrapper takes a recurrent layer (east.g. the first LSTM layer) as an statement.

It likewise allows yous to specify the merge mode, that is how the forward and astern outputs should exist combined before being passed on to the adjacent layer. The options are:

'sum': The outputs are added together.
'mul': The outputs are multiplied together.
'concat': The outputs are concatenated together (the default), providing double the number of outputs to the next layer.
'ave': The average of the outputs is taken.

The default mode is to concatenate, and this is the method oftentimes used in studies of bidirectional LSTMs.

Sequence Classification Problem

We will define a simple sequence classification problem to explore bidirectional LSTMs.

The problem is defined equally a sequence of random values betwixt 0 and 1. This sequence is taken as input for the trouble with each number provided i per timestep.

A binary characterization (0 or i) is associated with each input. The output values are all 0. In one case the cumulative sum of the input values in the sequence exceeds a threshold, and then the output value flips from 0 to one.

A threshold of 1/four the sequence length is used.

For example, beneath is a sequence of 10 input timesteps (X):

0.63144003 0.29414551 0.91587952 0.95189228 0.32195638 0.60742236 0.83895793 0.18023048 0.84762691 0.29165514

The corresponding classification output (y) would exist:

We can implement this in Python.

The offset step is to generate a sequence of random values. We can utilize the random() role from the random module.

# create a sequence of random numbers in [0,1]

X = array ( [ random ( ) for _ in range ( 10 ) ] )

We can ascertain the threshold as 1-quarter the length of the input sequence.

# summate cut-off value to alter form values

limit = 10 / iv.0

The cumulative sum of the input sequence can be calculated using the cumsum() NumPy function. This function returns a sequence of cumulative sum values, e.chiliad.:

pos1, pos1+pos2, pos1+pos2+pos3, ...

Nosotros tin then calculate the output sequence equally whether each cumulative sum value exceeded the threshold.

# determine the class outcome for each item in cumulative sequence

y = assortment ( [ 0 if x < limit else 1 for x in cumsum ( X ) ] )

The function beneath, named get_sequence(), draws all of this together, taking as input the length of the sequence, and returns the X and y components of a new problem instance.

from random import random

from numpy import array

from numpy import cumsum

# create a sequence classification example

def get_sequence ( n_timesteps ) :

# create a sequence of random numbers in [0,ane]

X = array ( [ random ( ) for _ in range ( n_timesteps ) ] )

# calculate cutting-off value to change class values

limit = n_timesteps / iv.0

# determine the course upshot for each particular in cumulative sequence

y = array ( [ 0 if x < limit else one for x in cumsum ( X ) ] )

return X , y

Nosotros can test this function with a new 10 timestep sequence equally follows:

X , y = get_sequence ( 10 )

print ( Ten )

print ( y )

Running the instance first prints the generated input sequence followed by the matching output sequence.

[ 0.22228819 0.26882207 0.069623 0.91477783 0.02095862 0.71322527

0.90159654 0.65000306 0.88845226 0.4037031 ]

[0 0 0 0 0 0 1 one ane 1]

LSTM For Sequence Nomenclature

We tin outset off by developing a traditional LSTM for the sequence classification trouble.

Firstly, we must update the get_sequence() function to reshape the input and output sequences to be iii-dimensional to meet the expectations of the LSTM. The expected structure has the dimensions [samples, timesteps, features].

The nomenclature problem has ane sample (e.chiliad. ane sequence), a configurable number of timesteps, and i feature per timestep.

Therefore, we can reshape the sequences equally follows.

# reshape input and output data to be suitable for LSTMs

10 = X . reshape ( 1 , n_timesteps , 1 )

y = y . reshape ( ane , n_timesteps , 1 )

The updated get_sequence() function is listed below.

# create a sequence classification instance

def get_sequence ( n_timesteps ) :

# create a sequence of random numbers in [0,one]

X = array ( [ random ( ) for _ in range ( n_timesteps ) ] )

# calculate cut-off value to change course values

limit = n_timesteps / iv.0

# determine the grade result for each item in cumulative sequence

y = array ( [ 0 if 10 < limit else one for x in cumsum ( X ) ] )

# reshape input and output data to be suitable for LSTMs

X = X . reshape ( i , n_timesteps , 1 )

y = y . reshape ( i , n_timesteps , 1 )

return X , y

We volition define the sequences as having 10 timesteps.

Next, we tin ascertain an LSTM for the problem. The input layer will have x timesteps with ane feature a piece, input_shape=(10, ane).

The commencement hidden layer volition have 20 retentiveness units and the output layer will be a fully continued layer that outputs one value per timestep. A sigmoid activation office is used on the output to predict the binary value.

A TimeDistributed wrapper layer is used around the output layer so that one value per timestep can exist predicted given the full sequence provided every bit input. This requires that the LSTM subconscious layer returns a sequence of values (one per timestep) rather than a unmarried value for the whole input sequence.

Finally, considering this is a binary nomenclature trouble, the binary log loss (binary_crossentropy in Keras) is used. The efficient ADAM optimization algorithm is used to detect the weights and the accuracy metric is calculated and reported each epoch.

# define LSTM

model = Sequential ( )

model . add ( LSTM ( 20 , input_shape = ( 10 , 1 ) , return_sequences = True ) )

model . add ( TimeDistributed ( Dense ( 1 , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' , metrics = [ 'accuracy' ] )

The LSTM will be trained for 1,000 epochs. A new random input sequence volition be generated each epoch for the network to be fit on. This ensures that the model does not memorize a single sequence and instead can generalize a solution to solve all possible random input sequences for this trouble.

# train LSTM

for epoch in range ( k ) :

# generate new random sequence

X , y = get_sequence ( n_timesteps )

# fit model for 1 epoch on this sequence

model . fit ( X , y , epochs = ane , batch_size = 1 , verbose = two )

Once trained, the network will be evaluated on yet another random sequence. The predictions volition exist then compared to the expected output sequence to provide a concrete example of the skill of the system.

# evaluate LSTM

X , y = get_sequence ( n_timesteps )

yhat = model . predict_classes ( X , verbose = 0 )

for i in range ( n_timesteps ) :

print ( 'Expected:' , y [ 0 , i ] , 'Predicted' , yhat [ 0 , i ] )

The complete example is listed below.

iii

vii

fourteen

xxx

from random import random

from numpy import array

from numpy import cumsum

from keras . models import Sequential

from keras . layers import LSTM

from keras . layers import Dense

from keras . layers import TimeDistributed

# create a sequence classification example

def get_sequence ( n_timesteps ) :

# create a sequence of random numbers in [0,one]

X = array ( [ random ( ) for _ in range ( n_timesteps ) ] )

# calculate cut-off value to alter class values

limit = n_timesteps / 4.0

# determine the class outcome for each item in cumulative sequence

y = array ( [ 0 if x < limit else 1 for x in cumsum ( X ) ] )

# reshape input and output data to be suitable for LSTMs

X = X . reshape ( 1 , n_timesteps , ane )

y = y . reshape ( 1 , n_timesteps , 1 )

return 10 , y

# define problem properties

n_timesteps = 10

# ascertain LSTM

model = Sequential ( )

model . add ( LSTM ( twenty , input_shape = ( n_timesteps , 1 ) , return_sequences = True ) )

model . add together ( TimeDistributed ( Dense ( i , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' , metrics = [ 'accuracy' ] )

# railroad train LSTM

for epoch in range ( grand ) :

# generate new random sequence

X , y = get_sequence ( n_timesteps )

# fit model for one epoch on this sequence

model . fit ( X , y , epochs = 1 , batch_size = 1 , verbose = 2 )

# evaluate LSTM

10 , y = get_sequence ( n_timesteps )

yhat = model . predict_classes ( X , verbose = 0 )

for i in range ( n_timesteps ) :

print ( 'Expected:' , y [ 0 , i ] , 'Predicted' , yhat [ 0 , i ] )

Running the case prints the log loss and classification accuracy on the random sequences each epoch.

This provides a clear idea of how well the model has generalized a solution to the sequence classification trouble.

Annotation: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average consequence.

We can see that the model does well, achieving a last accuracy that hovers effectually 90% and 100% accurate. Not perfect, just proficient for our purposes.

The predictions for a new random sequence are compared to the expected values, showing a mostly correct issue with a single error.

half-dozen

viii

thirteen

xiv

twenty

...

Epoch 1/1

0s - loss: 0.2039 - acc: 0.9000

Epoch 1/1

0s - loss: 0.2985 - acc: 0.9000

Epoch one/1

0s - loss: 0.1219 - acc: one.0000

Epoch 1/1

0s - loss: 0.2031 - acc: 0.9000

Epoch 1/1

0s - loss: 0.1698 - acc: 0.9000

Expected: [0] Predicted [0]

Expected: [0] Predicted [i]

Expected: [one] Predicted [i]

Expected: [1] Predicted [1]

Expected: [1] Predicted [one]

Expected: [ane] Predicted [1]

Bidirectional LSTM For Sequence Classification

Now that nosotros know how to develop an LSTM for the sequence classification problem, we can extend the example to demonstrate a Bidirectional LSTM.

We can practice this past wrapping the LSTM subconscious layer with a Bidirectional layer, as follows:

model . add ( Bidirectional ( LSTM ( twenty , return_sequences = True ) , input_shape = ( n_timesteps , 1 ) ) )

This volition create two copies of the subconscious layer, ane fit in the input sequences as-is and i on a reversed re-create of the input sequence. Past default, the output values from these LSTMs will be concatenated.

That means that instead of the TimeDistributed layer receiving ten timesteps of xx outputs, it volition now receive 10 timesteps of xl (20 units + 20 units) outputs.

The complete example is listed below.

five

seven

nine

fourteen

sixteen

eighteen

thirty

from random import random

from numpy import array

from numpy import cumsum

from keras . models import Sequential

from keras . layers import LSTM

from keras . layers import Dense

from keras . layers import TimeDistributed

from keras . layers import Bidirectional

# create a sequence classification instance

def get_sequence ( n_timesteps ) :

# create a sequence of random numbers in [0,ane]

10 = assortment ( [ random ( ) for _ in range ( n_timesteps ) ] )

# calculate cut-off value to alter class values

limit = n_timesteps / four.0

# decide the form outcome for each item in cumulative sequence

y = array ( [ 0 if x < limit else one for ten in cumsum ( X ) ] )

# reshape input and output information to be suitable for LSTMs

X = X . reshape ( 1 , n_timesteps , 1 )

y = y . reshape ( 1 , n_timesteps , 1 )

return X , y

# define problem properties

n_timesteps = ten

# ascertain LSTM

model = Sequential ( )

model . add ( Bidirectional ( LSTM ( 20 , return_sequences = True ) , input_shape = ( n_timesteps , ane ) ) )

model . add together ( TimeDistributed ( Dense ( 1 , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' , metrics = [ 'accurateness' ] )

# train LSTM

for epoch in range ( yard ) :

# generate new random sequence

Ten , y = get_sequence ( n_timesteps )

# fit model for one epoch on this sequence

model . fit ( X , y , epochs = 1 , batch_size = 1 , verbose = 2 )

# evaluate LSTM

X , y = get_sequence ( n_timesteps )

yhat = model . predict_classes ( 10 , verbose = 0 )

for i in range ( n_timesteps ) :

print ( 'Expected:' , y [ 0 , i ] , 'Predicted' , yhat [ 0 , i ] )

Running the example, nosotros see a similar output as in the previous example.

The employ of bidirectional LSTMs have the effect of allowing the LSTM to learn the trouble faster.

This is not apparent from looking at the skill of the model at the terminate of the run, but instead, the skill of the model over time.

seven

...

Epoch ane/one

0s - loss: 0.0967 - acc: 0.9000

Epoch 1/1

0s - loss: 0.0865 - acc: 1.0000

Epoch 1/one

0s - loss: 0.0905 - acc: 0.9000

Epoch 1/one

0s - loss: 0.2460 - acc: 0.9000

Epoch 1/i

0s - loss: 0.1458 - acc: 0.9000

Expected: [0] Predicted [0]

Expected: [1] Predicted [1]

Expected: [ane] Predicted [1]

Expected: [one] Predicted [1]

Expected: [ane] Predicted [1]

Compare LSTM to Bidirectional LSTM

In this example, we will compare the performance of traditional LSTMs to a Bidirectional LSTM over time while the models are being trained.

Nosotros will adjust the experiment so that the models are only trained for 250 epochs. This is so that nosotros can become a articulate idea of how learning unfolds for each model and how the learning behavior differs with bidirectional LSTMs.

We volition compare three unlike models; specifically:

LSTM (as-is)
LSTM with reversed input sequences (eastward.grand. you lot can do this by setting the "go_backwards" statement to he LSTM layer to "True")
Bidirectional LSTM

This comparison will aid to show that bidirectional LSTMs can in fact add together something more than but reversing the input sequence.

We volition ascertain a function to create and return an LSTM with either forward or astern input sequences, as follows:

def get_lstm_model ( n_timesteps , backwards ) :

model = Sequential ( )

model . add ( LSTM ( twenty , input_shape = ( n_timesteps , 1 ) , return_sequences = True , go_backwards = backwards ) )

model . add ( TimeDistributed ( Dense ( one , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' )

return model

We can develop a similar office for bidirectional LSTMs where the merge style tin can be specified as an argument. The default of chain can exist specified past setting the merge mode to the value 'concat'.

def get_bi_lstm_model ( n_timesteps , mode ) :

model = Sequential ( )

model . add ( Bidirectional ( LSTM ( xx , return_sequences = True ) , input_shape = ( n_timesteps , one ) , merge_mode = style ) )

model . add ( TimeDistributed ( Dumbo ( 1 , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' )

return model

Finally, nosotros define a function to fit a model and retrieve and store the loss each training epoch, then render a list of the collected loss values after the model is fit. This is so that we tin graph the log loss from each model configuration and compare them.

def train_model ( model , n_timesteps ) :

loss = list ( )

for _ in range ( 250 ) :

# generate new random sequence

X , y = get_sequence ( n_timesteps )

# fit model for one epoch on this sequence

hist = model . fit ( X , y , epochs = 1 , batch_size = 1 , verbose = 0 )

loss . suspend ( hist . history [ 'loss' ] [ 0 ] )

return loss

Putting this all together, the complete example is listed beneath.

Get-go a traditional LSTM is created and fit and the log loss values plot. This is repeated with an LSTM with reversed input sequences and finally an LSTM with a concatenated merge.

two

five

half-dozen

vii

viii

nine

xiv

xvi

xviii

thirty

fifty

sixty

from random import random

from numpy import array

from numpy import cumsum

from matplotlib import pyplot

from pandas import DataFrame

from keras . models import Sequential

from keras . layers import LSTM

from keras . layers import Dense

from keras . layers import TimeDistributed

from keras . layers import Bidirectional

# create a sequence classification instance

def get_sequence ( n_timesteps ) :

# create a sequence of random numbers in [0,ane]

X = array ( [ random ( ) for _ in range ( n_timesteps ) ] )

# summate cut-off value to modify course values

limit = n_timesteps / 4.0

# determine the form consequence for each item in cumulative sequence

y = assortment ( [ 0 if x < limit else 1 for x in cumsum ( X ) ] )

# reshape input and output data to be suitable for LSTMs

X = Ten . reshape ( 1 , n_timesteps , 1 )

y = y . reshape ( ane , n_timesteps , 1 )

return Ten , y

def get_lstm_model ( n_timesteps , backwards ) :

model = Sequential ( )

model . add ( LSTM ( 20 , input_shape = ( n_timesteps , 1 ) , return_sequences = True , go_backwards = backwards ) )

model . add ( TimeDistributed ( Dense ( 1 , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' )

return model

def get_bi_lstm_model ( n_timesteps , mode ) :

model = Sequential ( )

model . add ( Bidirectional ( LSTM ( twenty , return_sequences = True ) , input_shape = ( n_timesteps , 1 ) , merge_mode = mode ) )

model . add ( TimeDistributed ( Dumbo ( 1 , activation = 'sigmoid' ) ) )

model . compile ( loss = 'binary_crossentropy' , optimizer = 'adam' )

return model

def train_model ( model , n_timesteps ) :

loss = listing ( )

for _ in range ( 250 ) :

# generate new random sequence

X , y = get_sequence ( n_timesteps )

# fit model for i epoch on this sequence

hist = model . fit ( Ten , y , epochs = one , batch_size = 1 , verbose = 0 )

loss . append ( hist . history [ 'loss' ] [ 0 ] )

render loss

n_timesteps = ten

results = DataFrame ( )

# lstm frontward

model = get_lstm_model ( n_timesteps , Fake )

results [ 'lstm_forw' ] = train_model ( model , n_timesteps )

# lstm backwards

model = get_lstm_model ( n_timesteps , True )

results [ 'lstm_back' ] = train_model ( model , n_timesteps )

# bidirectional concat

model = get_bi_lstm_model ( n_timesteps , 'concat' )

results [ 'bilstm_con' ] = train_model ( model , n_timesteps )

# line plot of results

results . plot ( )

pyplot . show ( )

Running the case creates a line plot.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation process, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the LSTM forrad (blue) and LSTM backward (orangish) prove like log loss over the 250 training epochs.

Nosotros can see that the Bidirectional LSTM log loss is different (dark-green), going down sooner to a lower value and generally staying lower than the other ii configurations.

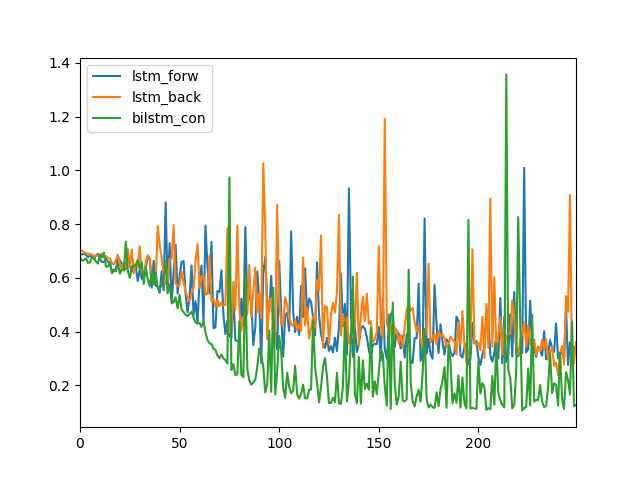
Line Plot of Log Loss for an LSTM, Reversed LSTM and a Bidirectional LSTM

Comparing Bidirectional LSTM Merge Modes

At that place a 4 dissimilar merge modes that can be used to combine the outcomes of the Bidirectional LSTM layers.

They are concatenation (default), multiplication, average, and sum.

We can compare the beliefs of dissimilar merge modes by updating the example from the previous section every bit follows:

thirteen

n_timesteps = 10

results = DataFrame ( )

# sum merge

model = get_bi_lstm_model ( n_timesteps , 'sum' )

results [ 'bilstm_sum' ] = train_model ( model , n_timesteps )

# mul merge

model = get_bi_lstm_model ( n_timesteps , 'mul' )

results [ 'bilstm_mul' ] = train_model ( model , n_timesteps )

# avg merge

model = get_bi_lstm_model ( n_timesteps , 'ave' )

results [ 'bilstm_ave' ] = train_model ( model , n_timesteps )

# concat merge

model = get_bi_lstm_model ( n_timesteps , 'concat' )

results [ 'bilstm_con' ] = train_model ( model , n_timesteps )

# line plot of results

results . plot ( )

pyplot . evidence ( )

Running the instance will create a line plot comparison the log loss of each merge mode.

The different merge modes consequence in dissimilar model performance, and this volition vary depending on your specific sequence prediction trouble.

In this case, nosotros tin come across that perhaps a sum (blue) and concatenation (reddish) merge style may event in better performance, or at to the lowest degree lower log loss.

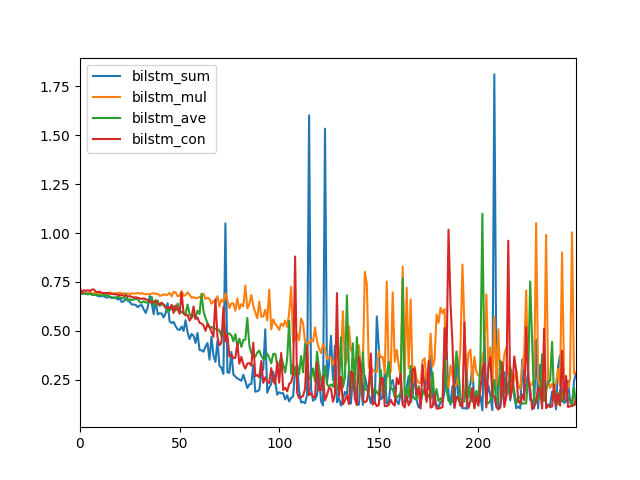
Line Plot to Compare Merge Modes for Bidirectional LSTMs

Summary

In this tutorial, you discovered how to develop Bidirectional LSTMs for sequence classification in Python with Keras.

Specifically, y'all learned:

How to develop a contrived sequence classification trouble.
How to develop an LSTM and Bidirectional LSTM for sequence classification.
How to compare merge modes for Bidirectional LSTMs for sequence classification.

Practise y'all accept any questions?
Ask your questions in the comments below and I will exercise my best to respond.

Develop LSTMs for Sequence Prediction Today!

Develop Your Own LSTM models in Minutes

...with just a few lines of python code

Find how in my new Ebook:
Long Short-Term Retentivity Networks with Python

Information technology provides self-study tutorials on topics like:
CNN LSTMs, Encoder-Decoder LSTMs, generative models, information preparation, making predictions and much more...

Finally Bring LSTM Recurrent Neural Networks to
Your Sequence Predictions Projects

Skip the Academics. Just Results.

See What'due south Within